Was sind Neuronale Netze

Neuronale Netze bilden das digitale Pendant zu unserem menschlichen Gehirn. Sie ähneln ihm sowohl im Aufbau als auch in ihrer Lern- und Funktionsweise. Sie sind ein Teil der Technologien, die im Machine Learning verwendet werden und bilden die Grundlage für das Deep Learning. Durch eben diese Anwendungsfelder sind neuronale Netze großer Bestandteil von vielen Anwendungen unseres Alltags. Wir nehmen sie jedoch gar nicht direkt wahr, da sie immer hinter Sprachassistenten und schönen Oberflächen, wie beispielsweise beim Business Namen Generator namelix, verpackt sind. Da sie uns so stark beeinflussen, möchten wir euch in diesem Blogartikel eine Einführung darüber geben, was neuronale Netze sind, wie sie funktionieren und auch wie sie lernen.

Was sind neuronale Netze?

Neuronale Netze, oder besser gesagt künstliche neuronale Netze (KNN) sind Algorithmen. Diese bilden die Funktionsweise des menschlichen Gehirns in der digitalen Welt ab.

Wie beim Gehirn bestehen auch KNN aus einem Netzwerk von Knoten. In unserem Gehirn sind dies die Nervenzellen, die durch Synapsen miteinander verknüpft sind. In KNN sind diese Knoten Neuronen, die algorithmisch bzw. mathematisch zu einem Netzwerk verbunden werden. Die Gewichtung dieser Verbindungen definiert hierbei, wie wichtig eine Verbindung im Netzwerk ist. Durch das Trainieren des KNN passt sich diese Gewichtung an und kann sich im Laufe des Trainings verändern.

Künstliche neuronale Netze finden häufig Verwendung im Machine Learning und sind die Hauptkomponente des dazugehörigen Deep Learning. In diesen Bereichen haben sich viele Anwendungsfälle entwickelt, wie zum Beispiel:

Wie sind neuronale Netze aufgebaut?

Künstliche neuronale Netze bestehen in der Regel aus Neuronen, die sich zu 3 Schichten zuordnen lassen:

Die Eingabeschicht nimmt die Eingabeinformation, wie beispielsweise Bilder von Hunden und Katzen, auf. Diese werden dann als Wert an das Netz bzw. die nachfolgenden verborgenen Schichten weitergegeben. Die verborgenen Schichten, von denen es beliebig viele geben kann, errechnen anhand der vorhandenen Informationen die Ausgabe. Bei diesem Beispiel wird die Wahrscheinlichkeit des Auftretens eines Hundes und einer Katze angegeben. Diese wird über die Ausgabeschicht wieder vom Netz ausgegeben.

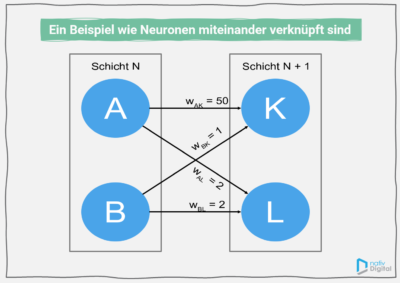
Die Neuronen sind hierbei durch gewichtete Verbindungen miteinander verknüpft, was zum Beispiel wie in folgendem Bild aussehen könnte:

In diesem Beispiel hat das Neuron A mehr Einfluss auf das Neuron K. Die Gewichtung von 50 ist größer als die Gewichtung von B auf K. Hingegen haben die Neuronen A und B den gleichen Einfluss auf das Neuron L, da die Gewichtungen gleich sind.

Wie funktionieren neuronale Netze?

Im Grunde müssen wir bei künstlichen neuronalen Netzen die Funktionsweise auf zwei unterschiedliche Art und Weisen betrachten. Einerseits auf Neuronen- bzw. Knoten-Ebene und andererseits auf Netzebene.

Funktionsweise auf Netzebene

Am einfachsten lässt sich die Funktionsweise auf Netzwerkebene erklären. Das KNN erhält eine Eingabe und berechnet mit dieser die Ausgabe. Dabei bildet sich die Eingabe jeder Schicht aus der Ausgabe der vorherigen Schicht. Zusätzlich werden hier die Eingabewerte für jede Schicht noch gewichtet, wie wir euch beim Aufbau von neuronalen Netzen gezeigt haben.

Beispielsweise könnten die Eingabedaten Bilder von Tieren sein, die identifiziert werden sollen. Diese werden in Daten umgewandelt, mit welcher das Netz rechnen kann. Das Netz berechnet mit seinen Schichten und den Bilddaten eine Wahrscheinlichkeit dafür, welches Tier auf dem Bild zu sehen ist.

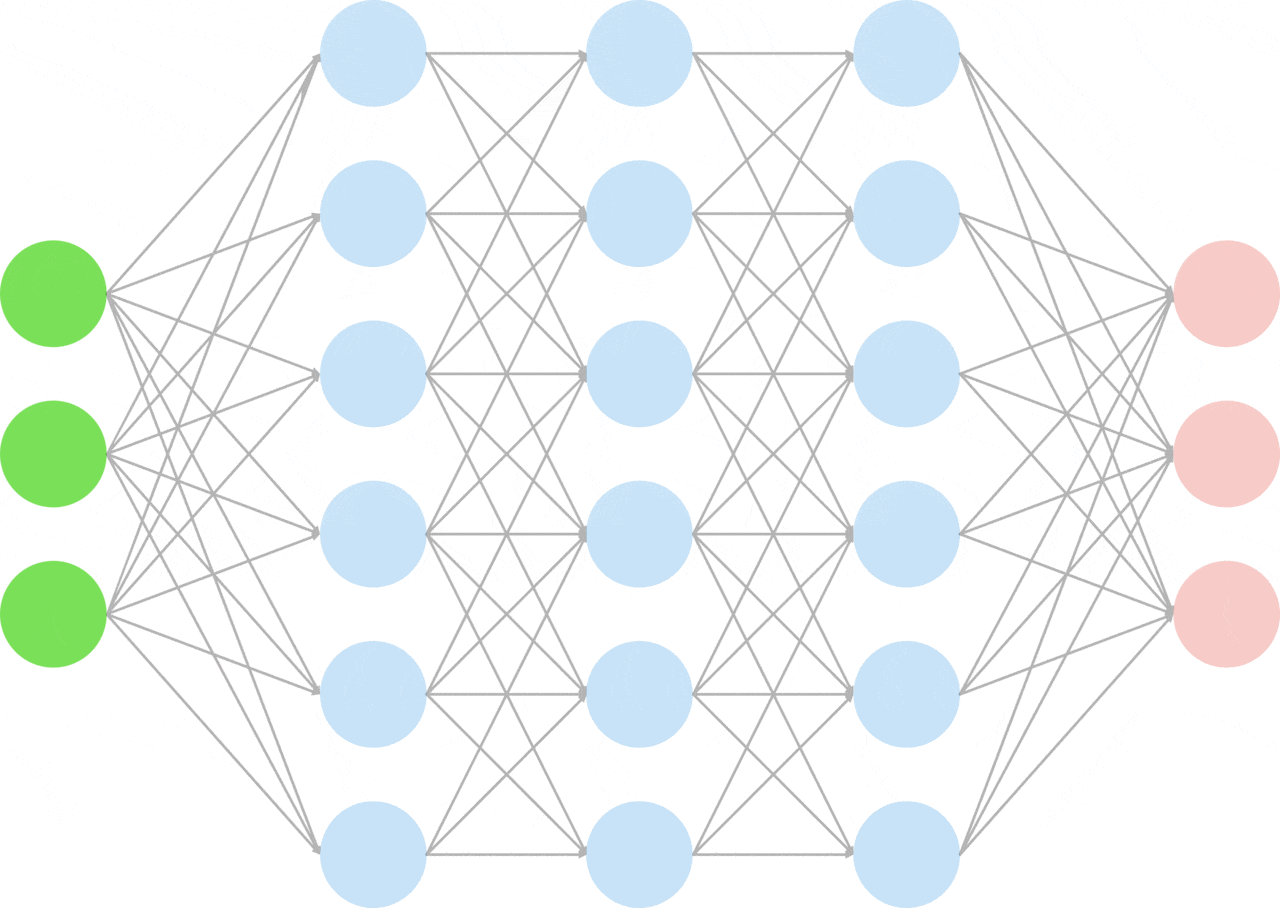
Grundlegend ist die Funktionsweise bei allen Netzarten so, wie es die Animation darstellt. Unterschiede zwischen den Arten liegen beispielsweise in der Architektur des Netzes, aber auch in der unterschiedlichen Funktionsweise auf Knotenebene.

Einen kleinen Überblick über die unterschiedlichen Arten von neuronalen Netzen geben wir euch später in diesem Blogartikel.

Funktionsweise auf Knotenebene

Wie die Funktionsweise auf Knotenebene ist, lässt sich in vereinfachter Art im folgenden Bild erklären:

Jeder Knoten erhält eine Menge von Eingaben, die wir hier als x bezeichnen. Jede dieser Eingaben hat ein Gewicht, in unserem Fall mit w betitelt. Werden Gewichtung w und Wert x multipliziert, dann erhalten wir die gewichtete Eingabe. Aus dieser ergibt sich die tatsächliche Eingabe für den Knoten, indem alle gewichteten Eingaben aufsummiert werden. Diese aufsummierte Aufgabe bestimmt nun mithilfe der Aktivierungsfunktion die Ausgabe des Neurons (Y).

Bei der Aktivierungsfunktion handelt es sich um Funktionen, die den möglichen Ausgabewert, also den Wertebereich der Ausgabe bestimmen. Beispielsweise bildet eine lineare Abbildungsfunktion den Wert auf sich selbst ab. Der Wertebereich wird also nicht beschränkt. Andere bekannte Funktionen sind die Sigmoid-Funktion oder die ReLU-Funktion (kurz für Rectified Linear Unit). Stellt man diese Funktionen nun als Graphen dar, wird deutlich, wie sich die Auswahl auf den Ausgabewert auswirkt.

Doch warum gibt es unterschiedliche Aktivierungsfunktionen? Einerseits ist es für nachfolgende Schichten im Netz notwendig, dass die Ausgabe der vorherigen Neuronen zwischen 0 und 1 liegen. Ist diese der Fall, dann wird beispielsweise die Sigmoid Funktion verwendet. Andererseits können Aktivierungsfunktionen, wie die ReLU-Funktion bestimmten auftretenden Problemen, wie dem explodierenden oder verschwindenden Gradienten entgegenwirken.

Wir haben hier, wie angekündigt, die einfachste Form des Knotens beschrieben. Teilweise gibt es komplexerer Knoten, die neben den gewichteten Eingaben der vorherigen Schicht noch weitere Eingaben benötigen. Ein bekanntes Beispiel hierfür ist der Long Short Term Memory (LSTM)-Knoten. Dieser erhält nicht nur die gewichteten Eingaben w ∙ x, sondern auch noch die Ausgabe, die sie im vorherigen Schritt berechnet haben. Dadurch ist es möglich mit LSTM-Knoten eine Art Gedächtnis im neuronalen Netz zu erstellen.

Wie werden neuronale Netze trainiert?

Die Basis für das Training von neuronalen Netzen bilden die notwendigen Daten. Dies sind häufig recht große Datensätze, für die das erwartete Ergebnis bereits bekannt ist. Beispielsweise könnten solche Datensätze aus 10.000 Bildern von Hunden und Katzen bestehen.  Dabei ist bei jedem Bild bekannt, ob Katze oder Hund zu sehen ist. Dieser Datensatz wird in einen Trainingsdatensatz und einen Testdatensatz aufgeteilt. Die Trainingsdaten werden wie der Name bereits vermuten lässt verwendet, um das Netz zu trainieren. Die Testdaten hingegen um zu überprüfen, welche Ergebnisse das Netz mit fremden Daten liefert.

Die Trainingsmethode, die wir euch vorstellen wollen, wird als gradientenbasierte Optimierung bezeichnet. Diese besteht aus drei Schritten, die immer wieder über mehrere Epochen hinweg durchgeführt werden. Als Epoche wird hierbei das Durchlaufen der drei Schritte von allen Trainingsdaten bezeichnet. Die Anzahl der Epochen wird von den Entwickler*innen im Vorhinein festgelegt und bestimmt letztendlich die Trainingsdauer des Netzes.

Welche Arten von neuronalen Netzen gibt es?

Grundsätzlich gibt es viele Arten von künstlichen neuronalen Netzen. Wir wollen in diesem Blogbeitrag jedoch nur auf die einfachsten eingehen. Wenn ihr einen guten Überblick über die verschiedenen Arten haben wollt, bietet The Asimov Institute mit ihrem Cheatsheet über die Architekturen von künstlichen neuronalen Netzen eine gute Übersicht dazu an.

Die bekanntesten dieser Arten sind jedoch folgende:

Fazit

Aufgrund der vielen Arten künstlicher neuronaler Netze, ist der Anwendungsbereich vielseitig. Die sehr einfach dargestellten Beispiele über die Funktionsweise von künstlichen neuronalen Netzen geben euch einen ersten kleinen Einblick. Dahinter steckt weitaus mehr, die den Rahmen des Blogartikels jedoch sprengen würde.

Wenn ihr noch mehr über neuronale Netze wissen wollt und insbesondere mehr über die mathematischen Grundlagen der gradientenbasierten Optimierung erfahren wollt, findet ihr ausführliche Informationen dazu im Buch „Deep Learning“ von Goodfellow, Bengio und Courville.